QUESTION: (SUMMER2016) I am proportioning a mono-symmetric I-girder whose web-slenderness, h/w, marginally satisfies the Class 3 limit for W-shapes in pure bending in accordance with Table 2 of S16-09. Does this limit apply to mono-symmetric sections?
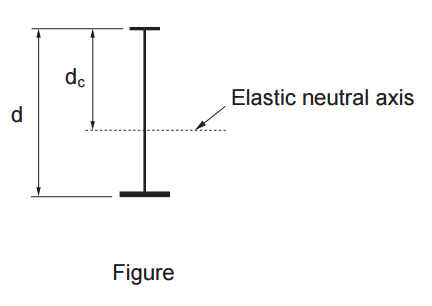
ANSWER: No, the limits for I-sections are provided in Table 2 of S16-09 for sections with equal flanges. CSA Standard S6, Canadian Highway Bridge Design Code, in Clause 10.10.3.1, addresses Class 3 web-limits for mono-symmetric I-sections. In this clause, the value of h is replaced by 2dc, where dc is the distance from the neutral axis to the compressive extreme fibre (see Figure).
QUESTION: (2014) I am calculating the laterally unsupported bending resistance of a singly symmetric I-section having flanges of unequal thickness. What should be the value of t in the expressions for βx and Cw provided in Sub-clause 13.6 (e) of S16-09?
ANSWER: In both expressions, the value for ʽd-tʼ may be taken as the centroidal distance between the flanges. Cw may also be calculated using the formula given under Built-up Sections in Part 6 of CISC Handbook of Steel Construction.
QUESTION: (FALL2012) How do I determine the elastic bending resistance of a cantilever plate subject to lateral-torsional buckling?
ANSWER: For a fix-ended plate subject to bending about its strong axis but laterally unbraced, the Guide to Stability Design Criteria for Metal Structures, 6th Edition (R.D. Ziemian, John Wiley & Sons, 2010) gives expressions for the elastic buckling moment (Mu), depending on the height of load application. For example, when subjected to a point load at its tip (see Figure):
a) For top surface loading:

where E and G are the elastic and shear modulii respectively, Iy is the minor-axis moment of inertia, J the St. Venant torsional constant, “d” the plate depth, and Lc the cantilever length.
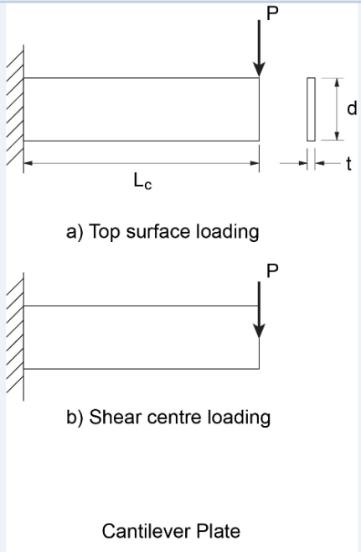 NOTE: In Advantage Steel #44, this column referenced the expressions for the elastic lateral-torsional buckling moment of cantilevers provided in the Guide to Stability Design Criteria for Metal Structures, 6th Edition. In comparison with recent studies using finite element analyses, the expression “Mc = 1.5GJ/d” gives unconservative values for plates (rectangular section) and long cantilevers of I-sections prone to lateral-torsional buckling. It should not be used for plate cantilevers significantly longer than twice their depth.
NOTE: In Advantage Steel #44, this column referenced the expressions for the elastic lateral-torsional buckling moment of cantilevers provided in the Guide to Stability Design Criteria for Metal Structures, 6th Edition. In comparison with recent studies using finite element analyses, the expression “Mc = 1.5GJ/d” gives unconservative values for plates (rectangular section) and long cantilevers of I-sections prone to lateral-torsional buckling. It should not be used for plate cantilevers significantly longer than twice their depth.
QUESTION: (SUMMER2012) In the design of continuous beams and Gerber beams can I assume the inflection points are laterally braced against lateral-torsional buckling?
ANSWER: One must not confuse the inflection points in the vertical bending moment diagram with the inflection points in the laterally buckled shape. In general, the buckled shape is not known at the design stage. Since the inflection points in the bending moment diagram generally do not coincide with those of the buckled shape they should not be taken as laterally braced unless they are braced.

