The bracing force, Pb, required to stabilize a laterally unsupported member is a function of several factors including the initial out-of-straightness or misalignment at the brace point, ΔO, and the displacement of the bracing system, Δb, according to S16-14 Clause 9.2.6.2:
![]()
where β is a coefficient that depends on the number of braces, Cf is the factored compression force, and Lb is the length between braces. The misalignment, ΔO, corresponds to the offset of a brace point relative to adjacent brace points. For the initial calculation of Pb , the brace displacement may be taken equal to the misalignment:
Δb = ΔO
The calculated brace displacement must not exceed ΔO unless justified by analysis. Since ΔO and Δb both depend on the misalignment, it is essential to evaluate its value correctly.
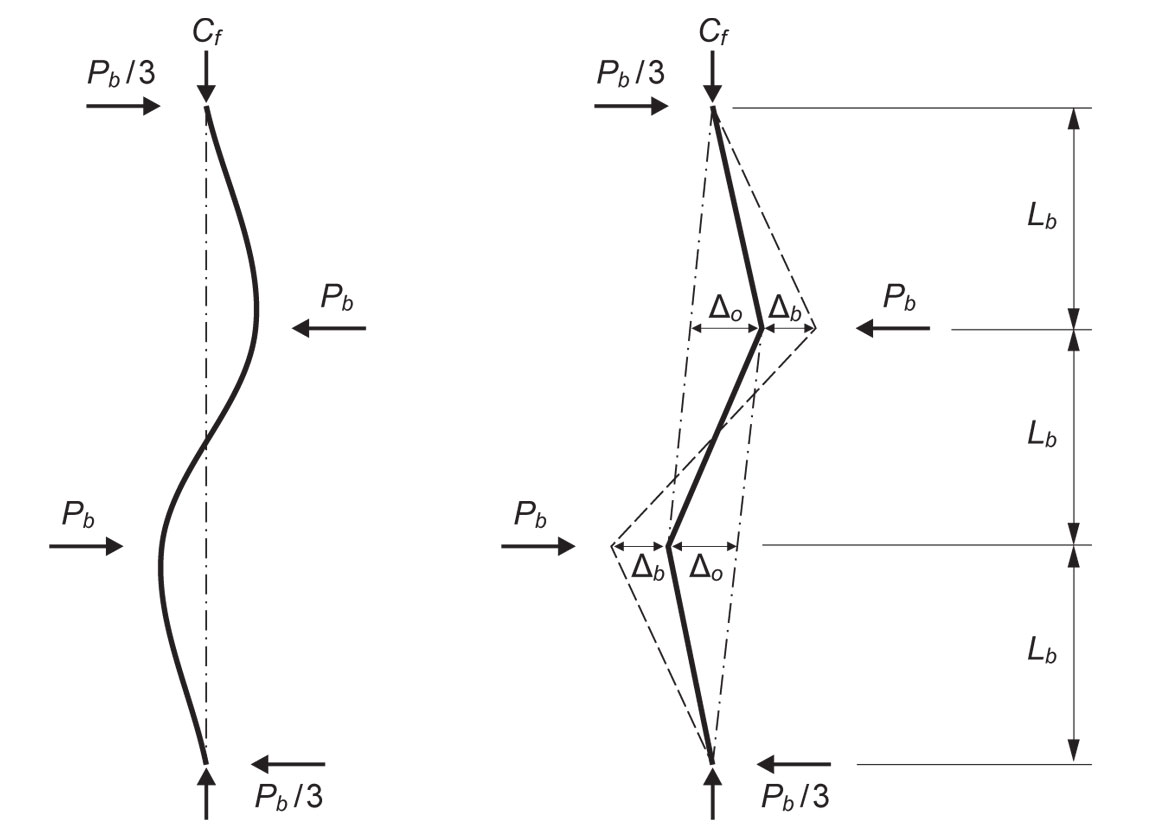
A member configuration involving two braces is illustrated in the accompanying figure. The solid line represents the initial misalignment, while the dotted line represents the final displaced configuration due to all the forces acting on the system.
As explained in the S16 Commentary to Clause 9.2.1, a common construction technique used to reduce the initial misalignment consists in pulling the structure within tolerance at brace locations, thus bringing columns into compliance with erection tolerances (Clause 29.3.7). As the structure is pulled into alignment, one brace point at the time, the resulting misalignment is the erection tolerance.
For exterior columns of multi-storey buildings and columns adjacent to elevator shafts (Clause 29.3.3), the misalignment is then:
ΔO = Lb / 1000
For other columns, the tolerance is:
ΔO = Lb / 500





