
Pour concevoir une poutre en acier selon l’article 13.6 de la norme CSA S16, on utilise souvent la valeur Lu, la plus longue longueur non soutenue pouvant permettre à la poutre d’atteindre Mr = φ Mp ou Mr = φ My, selon la classe de la section.
Autrement dit, lorsque la longueur non soutenue d’une poutre est inférieure à Lu, l’élément est considéré comme étant soutenu latéralement et atteint sa pleine capacité de moment. Lu figure également dans plusieurs tableaux de conception de la partie 5 du Handbook of Steel Construction, comme les tableaux de sélection et de charge des poutres.
Comme la norme S16 ne fournit pas d’expression explicite pour Lu, les ingénieurs se demandent parfois comment elle est dérivée. Pour calculer sa valeur, on suppose que la poutre est simplement supportée et soumise à un moment fléchissant uniforme, comme le montre la figure 1.

Figure 1
Dériver la formule Lu pour les poutres à ailes larges bisymétriques exige un peu d’algèbre. Une poutre de classe 1 ou 2 (résistance au moment maximale pondérée, Mr = φ Mp = φ Zx Fy) sera utilisée dans les calculs suivants.
La résistance au moment pondérée d’une poutre non soutenue latéralement est donnée par l’article 13.6(a) de la norme S16:19 :
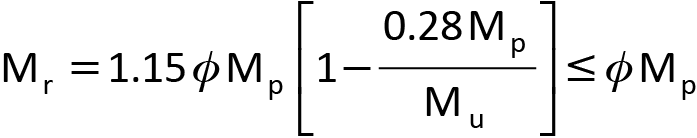
Éq. 1
lorsque Mu > 0,67 Mp. Mu est le moment de déversement élastique d’une poutre non contreventée latéralement de longueur L, qu’on obtient avec la formule :
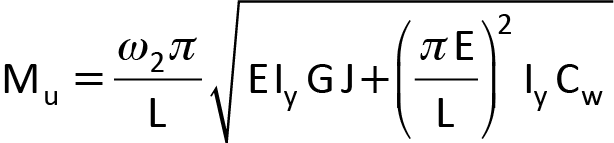
Éq. 2
et ω2 = 1,0 pour une poutre soumise à un moment uniforme.
Établir Mr = φ Mp dans l’équation 1 et remplacer l’expression par Mu de l’équation 2 :
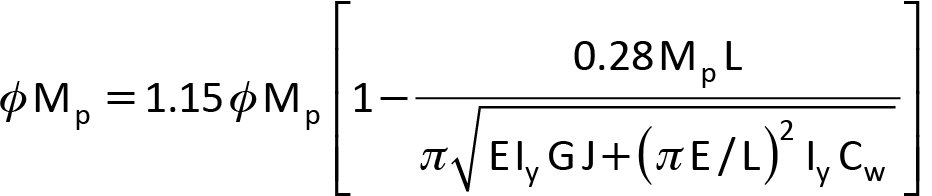
Éq. 3
Réorganisation de l’équation 3 pour que la racine carrée apparaisse du côté gauche :
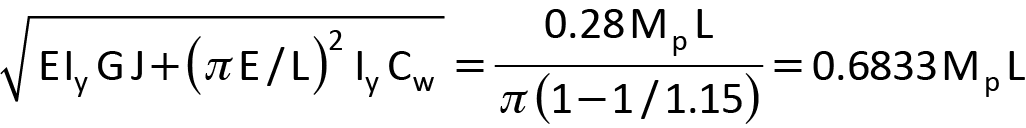
Éq. 4
Après avoir mis les deux côtés au carré et tout multiplié par L2, on obtient ce qui suit :
![]()
Éq. 5
Si X = L2, l’équation 5 est une expression quadratique de la forme :
![]()
Éq. 6
dont la solution est :
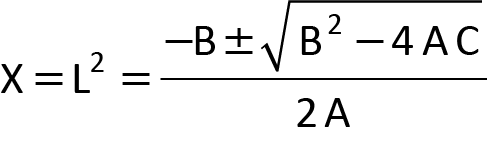
Éq. 7
Si nous identifions A, B et C dans l’équation 6 avec les termes correspondants dans l’équation 5, et que nous conservons le signe plus devant la racine carrée, l’équation 7 donne la solution suivante pour Lu :
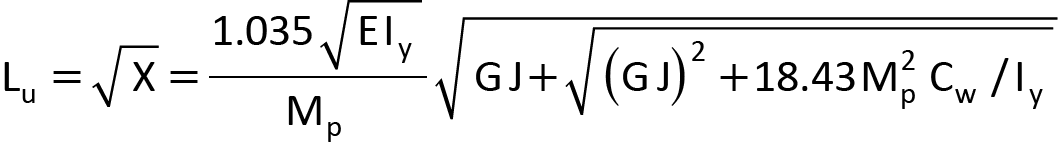
Éq. 8








